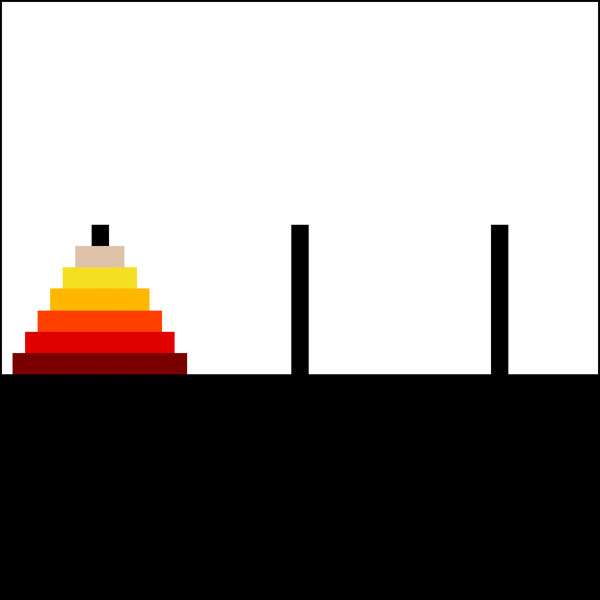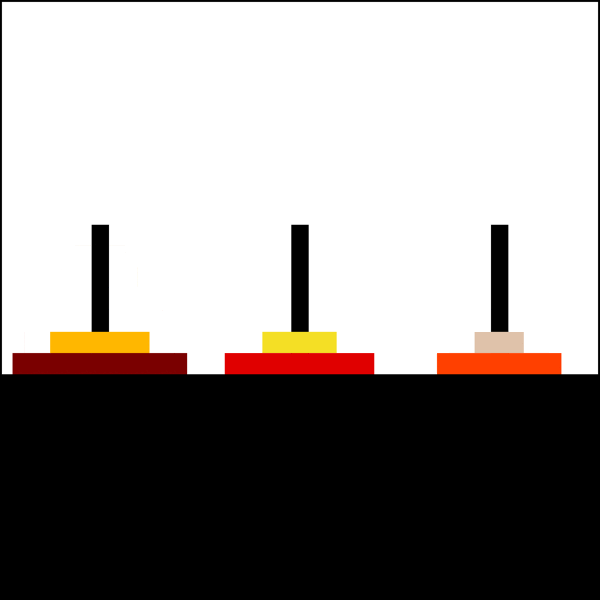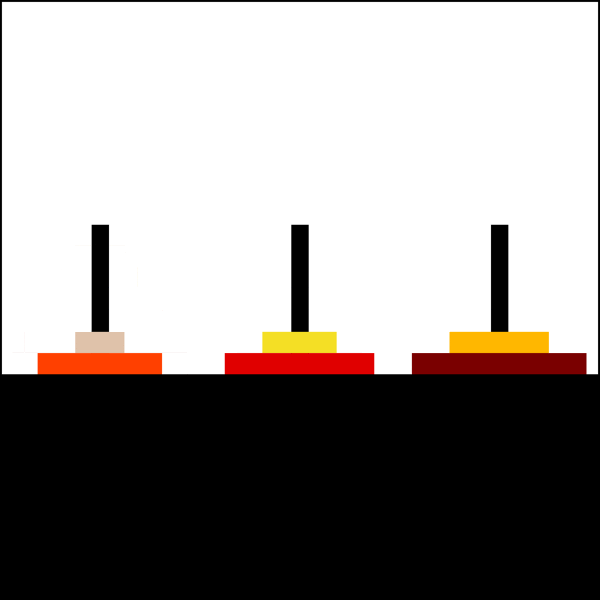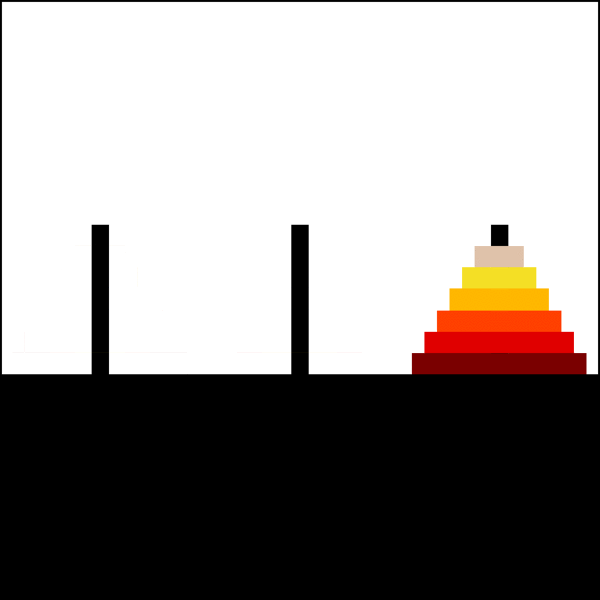Rubber Duck

I was first inspired by a great talk by Danny Lange from Unity at the GOTO 2018 conference titled ‘On the Road to Artificial General Intelligence’. In it, he argues (and shows!) how many problems can be solved using the framework of reinforcement learning, roughly by specifying the possible actions to take, and by providing a measure of reward at each state of the problem.

As a very simple example, I have used RL to solve the Tower of Hanoi¹. In the Tower of Hanoi, you have the task to move a number of disks from one pole (out of three) to another. However, you can only move one disk at a time, the disks vary in size, and it is only allowed to put smaller disks on top of larger ones.

For example, here’s a solution for a 6 disks Tower:

Source

I see it as a good starting problem, because it has a well-defined set of allowed actions and a precise state description.

Q-Learning

The center of Q-Learning is the Q-table. This table contains for all states, the expected reward when a given action is taken. The initial table will be all zeroes, because the agent doesn’t know anything about the environment yet. In the Tower of Hanoi, there will always be 6 different potential actions (even if not all are applicable at all times):

• top disk of pole 1 to top of pole 2
• top disk of pole 1 to top of pole 3
• top disk of pole 2 to top of pole 1
• top disk of pole 2 to top of pole 3
• top disk of pole 3 to top of pole 1
• top disk of pole 3 to top of pole 2

There will always be $3^\textit{# disks}$ possible states, so for only two disks, we have the following initial Q-table.

         ACTIONS
   [[0, 0, 0, 0, 0, 0]
    [0, 0, 0, 0, 0, 0]
S   [0, 0, 0, 0, 0, 0]
T   [0, 0, 0, 0, 0, 0]
A   [0, 0, 0, 0, 0, 0]
T   [0, 0, 0, 0, 0, 0]
E   [0, 0, 0, 0, 0, 0]
S   [0, 0, 0, 0, 0, 0]
    [0, 0, 0, 0, 0, 0]]

The Q-table acts as the policy for the agent. In reinforcement learning, the policy tells the agent what to do in each state. Right now, the Q-table is all zeroes, but as we will see, the Q-learning algorithm will update the Q-table with the expected reward by taking a specific action in each state. The policy is then to take the action with the largest expected reward.

Calculating Expected Rewards

We calculate the expected reward as a combination of the currently known reward value for a state and the new value, based on taking the best action in that state.

where

• $\alpha$ is the learning rate, which determines how valuable new information is compared to the existing information. When $\alpha$ is close to zero, the reward is reduced a lot, while when close to one, the old value is reduced a lot (since we subtract $Q(s_t, a)$).
• $\gamma$ is the discount factor, which determines how important expected future reward is. With a value close to zero, future rewards are diminished and the agent is shortsighted. A value closer to one will make the agent pursue long-term high rewards.

Depending on whether the environment is continuous or episodic, there can be different approaches. A continuous environment is one that continues forever. The agent will jump into the environment and will run until we stop it. An episodic environment, on the other hand, has a well-defined start and end, and the agent can use information gained in one episode to perform better in the next.

The Tower of Hanoi is clearly an episodic environment. It ends, when all the disks have been successfully moved to the correct pole. We can also specify that at most $n$ moves are allowed, so the episode ends when either the disks are in position, or the maximum steps have been reached.

We can now implement a Q-learning algorithm:

1. For each step choose an action based on the Q-table.
2. Take the action and observe the reward gained.
3. Update Q-table.

However, initially the Q-table is filled with zeroes, so what action should be chosen. This is in essence the exploration-exploitation tradeoff. Should we exploit what we know (getting the rewards we already know about), or should we explore the environment more, to potentially gain even larger rewards? The approach I will take here, is to initially only explore and then gradually, as we learn more about the environment, start to exploit (i.e. pick the best action in each state).

An implementation in Python

For the implementation, I use Gym, a toolkit for developing reinforcement learning algorithms. An environment in gym defines the state and action spaces, and makes it easy to iterate through multiple episodes of an episodic environment, or continuously update a continuous one. For Tower of Hanoi, I use an environment implemented by Robert Lange. It defines the possible actions and the state space, along with the reward function, which is very simple: Each step counts as zero, and the final state rewards 100 points.

Each state is a $n$-tuple, where $n$ is the number of disks. Each element in the tuple corresponds to a disk, and can have a value from 0 to 2, indicating what pole the disk is on. For $n=3$, the initial state is $(0,0,0)$ since all disks are stacked on the first pole. I convert this state to a number between $0-3^n$ to be able to update my Q-table in the state_to_q_state function.

Other than that, it is just a matter of running a bunch of episodes, decide whether to explore or exploit and then update the Q-table based on the result of the chosen action.

for episode in range(total_episodes):
    state = env.reset()  # reset environment each episode

    for step in range(max_steps):
        q_state = state_to_q_state(state)

        # decide if explore or exploit
        tradeoff = random.uniform(0, 1)

        if tradeoff > epsilon:
            action = np.argmax(qtable[q_state, :])
        else:
            action = env.action_space.sample()

        new_state, reward, done, info = env.step(action)

        q_new_state = state_to_q_state(new_state)
        qtable[q_state, action] = qtable[q_state, action] + 
                    learning_rate * (reward + 
                        gamma * np.max(qtable[q_new_state, :]) - qtable[q_state, action])

        state = new_state

        if done:
            break

    # update exploration-exploitation tradeoff limit
    epsilon = min_epsilon + (max_epsilon - min_epsilon) * np.exp(-decay_rate * episode)

Results

For 2-6 disks, the algorithm was quick to learn the best set of actions with the standard parameters I chose. How did I know it was the best? I changed the environment to give a reward of -1 for each action. The final reward is then $100-\textit{#num steps}+1$ (+1 because the final step does not subtract one, but adds 100). The output is as follows:

Number of Disks: 2
Score over time: 98.0
Number of Disks: 3
Score over time: 94.0
Number of Disks: 4
Score over time: 86.0
Number of Disks: 5
Score over time: 70.0
Number of Disks: 6
Score over time: 38.0

The optimal number of steps is $2^n - 1$ so we can verify that they are actually optimal.

For more than 6 disks (e.g. 7), we need to tweak. I specified max_steps=99 per default, but $2^7-1$ is 127, so we would need at least 127 steps. In reality we need more, because the algorithm needs to explore. It is possible to find parameters to do so, but for each new disk, we require many more steps to actually create the Q-table, so it is not very efficient. We will need to explore other approaches to reinforcement learning, like learning a more generic policy that would allow the agent to generalize to an arbitrary number of disks.

So - a fun little example, with a naive implementation that works for few disks, but gets problems as soon as we increase difficulty.

Links

• Repository
• Danny Lange @ GOTO 2018: On the Road to Artificial General Intelligence
• Deep Reinforcement Learning Course

Footnotes